Número é
um objeto da matemática usado para descrever quantidade, ordem ou medida. O
conceito de número provavelmente foi um dos primeiros conceitos matemáticos
assimilados pela humanidade no processo de contagem.
Para isto, os números naturais eram um bom começo. O
trabalho dos matemáticos nos levou a descobrir outros tipos de números. Os
números inteiros são uma extensão dos números naturais que incluem os números
inteiros negativos. Os números racionais, por sua vez, incluem frações de
inteiros. Os números reais são todos os números racionais mais os números
irracionais.
História dos números
O conceito de número está associada com a capacidade de
contar e comparar qual de dois conjuntos de entidades semelhantes é o maior. As
primeiras sociedades humanas encontraram dificuldades em determinar qual de
dois conjuntos era "maior" do que outro, ou para saber com precisão
quantos itens formavam uma coleção de coisas. Esses problemas podem ser
resolvidos com uma simples contagem. A maioria das culturas têm sistemas de
contagem que atingem pelo menos centenas, algumas outras mais simples têm
condições apenas de enumerar os números 1, 2 e 3 e usam o termo
"muitos" para quantidades maiores.
A contagem começou a ser feita usando objetos físicos
(tais como pilhas de pedras) e marcas como aquelas encontradas em ossos. Os
sistemas de numeração na maioria dos idiomas mostram que a contagem esta
associada aos dedos das mãos (sistema decimal).
Os registros de números com a utilização de símbolos
escritos é associado ao o surgimento de sociedades mais complexas aonde
passaram a ser necessários registros contábeis e burocráticos, registros
fiscais e de propriedade.
Tipos de
números
Os números podem ser classificados em conjunto de números que vem a ser uma coleção de elementos
Diferentes tipos de números podem ser digitados por
dois métodos diferentes, pelo método
construtivista ou através de axiomas. Pelo método construtivista é introduzido tipos
diferentes de números através da construção de um conjunto de elementos. Pelo
método axiomático é adotado um conjunto de postulados a partir dos quais e por dedução lógica,
são demonstrados teoremas.
 | Natural | 0, 1, 2, 3, 4, ... ou 1, 2, 3, 4, ... |
|---|---|---|
 | Inteiro | ..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, ... |
| - | Inteiro positivo | 1, 2, 3, 4, 5, ... |
 | Racional | a⁄b aonde a e b são inteiros e b é diferente dezero |
 | Real | Limite de uma sequência de números racionais convergentes |
 | Complexo | a + bi aonde a e b são números reais e i é araiz quadrada de −1 |
Número complexo
Um número complexo é um número  que pode ser escrito na forma
que pode ser escrito na forma 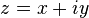 , em que
, em que  e
e  são números reais e
são números reais e  denota a unidade imaginária. Esta tem a propriedade
denota a unidade imaginária. Esta tem a propriedade  , sendo que
, sendo que  e
e  são chamados respectivamente parte real e parte imaginária de
são chamados respectivamente parte real e parte imaginária de  . O conjunto dos números complexos, denotado por
. O conjunto dos números complexos, denotado por  , contém o conjunto dos números reais.
, contém o conjunto dos números reais.
 que pode ser escrito na forma
que pode ser escrito na forma 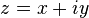 , em que
, em que  e
e  são números reais e
são números reais e  denota a unidade imaginária. Esta tem a propriedade
denota a unidade imaginária. Esta tem a propriedade  , sendo que
, sendo que  e
e  são chamados respectivamente parte real e parte imaginária de
são chamados respectivamente parte real e parte imaginária de  . O conjunto dos números complexos, denotado por
. O conjunto dos números complexos, denotado por  , contém o conjunto dos números reais.
, contém o conjunto dos números reais.
Os números complexos são utilizados em várias áreas do conhecimento, tais como engenharia, eletromagnetismo, física quântica, teoria do caos, além da própria matemática, em que são estudadas análise complexa, álgebra linear complexa, álgebra de Lie complexa, com aplicações em resolução de equações algébricas e equações diferenciais.
Número real
O conjunto dos números reais 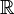 é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
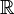 é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
Os números reais são números usados para representar uma quantidade contínua (incluindo o zero e os negativos).
Número racional
O conjunto dos números racionais (representado por Q, o uso da letra Q é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0).
Número inteiro
São constituídos dos números naturais, incluindo o zero (0, 1, 2, 3, ...) e dos simétricos dos números naturais não nulos (-1, -2, -3, ...). Dois números são simétricos se, e somente se, sua soma é zero. Por vezes, estes números são chamados de inteiros relativos.
O conjunto de todos os inteiros é representado por um Z em negrito (ou ainda um  em blackboard bold, ou ℤ, cujo código Unicode é U+2124), que vem do alemão Zahlen, que significa números, algarismos.
em blackboard bold, ou ℤ, cujo código Unicode é U+2124), que vem do alemão Zahlen, que significa números, algarismos.
 em blackboard bold, ou ℤ, cujo código Unicode é U+2124), que vem do alemão Zahlen, que significa números, algarismos.
em blackboard bold, ou ℤ, cujo código Unicode é U+2124), que vem do alemão Zahlen, que significa números, algarismos.
Os inteiros (juntamente com a operação de adição) formam o menor grupo que contém o monoide aditivo dos números naturais. Como os números naturais, os inteiros formam um conjunto infinito contável.
Número natural
Um número natural é um número inteiro não-negativo (0, 1, 2, 3,...). O número natural também é definido como um número inteiro positivo, aonde o zero não é considerado como um número natural. Quando o símbolo dos números naturais (N) vier seguido de um asterisco (*) é retirado o 0 (zero).
Número inteiro negativo
Número negativo é todo número real menor que zero, como o −1 e o −3. Dois números são chamados de números simétricos quando estão à mesma distância do zero, como o−5 e o 5.
Número fracionário
Fração é um modo de expressar uma quantidade a partir de um valor que é dividido por um determinado número de partes iguais entre si. Número fracionário expressa esta condição. A palavra vem do latim fractus e significa "partido", "quebrado" (do verbo frangere: "quebrar").
Número irracional
Número irracional é um número real que não pode ser obtido pela divisão de dois números inteiros, ou seja, são números reais mas não racionais. O conjunto dos números irracionais é representado pelo símbolo  .O conceito de número irracional remonta ao conceito de incomensurabilidade.
.O conceito de número irracional remonta ao conceito de incomensurabilidade.
 .O conceito de número irracional remonta ao conceito de incomensurabilidade.
.O conceito de número irracional remonta ao conceito de incomensurabilidade.
A primeira descoberta de um número irracional é geralmente atribuída a Hipaso de Metaponto, um seguidor de Pitágoras.
Número imaginário
Número imaginário é um número complexo com parte real igual a zero, ou seja, um número da forma b i, em que i é a unidade imaginária. Em alguns contextos, exige-se que bseja diferente de zero. O termo foi inventado por René Descartes em 1637 no seu La Géométrie para designar os números complexos em geral, e tem esse nome pelo objetivo inicialmente pejorativo: na época, acreditava-se que tais números não existissem .
Os números são fantásticos não? Contribuiu e continuará
para nossa evolução.



Nenhum comentário :
Postar um comentário